통계, 연구, 역학
Ordinary Least Squares 직관적으로 이해하기 - 3
Dr. yul
2025. 2. 3. 22:51
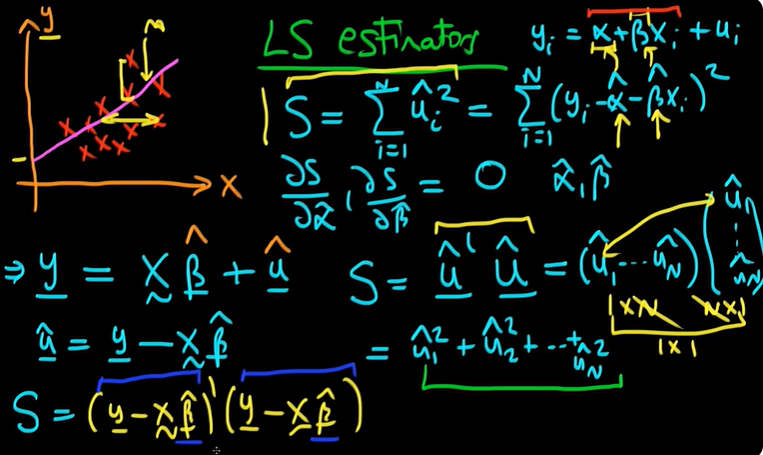
최소제곱법(OLS) 추정량의 행렬 유도 과정 요약
- 잔차 제곱합 (Sum of Squared Residuals, SSR) 표현
- 최소제곱법에서 목표는 잔차 제곱합 SS 를 최소화하는 것.
- 잔차 벡터 $\hat{u}$ 는 다음과 같이 정의됨:$\hat{u} = Y - X\hat{\beta}$
- 따라서 SSR은 다음과 같이 행렬식으로 표현됨:$S = \sum_{i=1}^{N} \hat{u}_i^2 = \hat{u}^T \hat{u} = (Y - X\hat{\beta})^T (Y - X\hat{\beta})$
- SSR의 전개 과정
- S를 전개하면 다음과 같은 4개의 항이 나타남:$S = Y^T Y - Y^T X \hat{\beta} - \hat{\beta}^T X^T Y + \hat{\beta}^T X^T X \hat{\beta}$
- 여기서, $Y^T Y$ 는 상수이므로 미분 시 사라짐.
- 두 번째 및 세 번째 항은 서로 전치(transpose) 관계이며, 최종적으로 $-2 X^T Y \hat{\beta}$ 로 표현 가능.
- 최적화 문제 (미분 및 정규방정식 도출)
- SSR을 최소화하기 위해 $\hat{\beta}$ 에 대해 미분:$\frac{dS}{d\hat{\beta}} = -2 X^T Y + 2 X^T X \hat{\beta} = 0$
- 이를 정리하면 OLS 추정량 (OLS Estimator) 유도:$X^T X \hat{\beta} = X^T Y$
- 최종적으로, 정규방정식의 해:$\hat{\beta} = (X^T X)^{-1} X^T Y$
- OLS의 기하학적 해석
- $\hat{Y} = X\hat{\beta}$ 는 Y 를 X 의 컬럼 스페이스에 직교 투영 한 값임.
- 즉, 잔차 벡터 $\hat{u}$ 는 컬럼 스페이스와 직교 해야 함:$X^T \hat{u} = 0$
- 이는 OLS가 잔차 제곱합을 최소화하는 방식을 수학적으로 설명하는 과정임.
출처: Ordinary Least Squares Estimators - derivation in matrix form - part 1